PAF Jobs As Commissioned Officer March 2023 Ad | Online Apply Details

 Stress & Strain 

Structure mechanics In Civil Engineering

Hello friends welcome to the lecture series of mechanics of material and the topic of today's lecture is normal stress. so if you understand this let's revisit our first problem using which we have rediscovered the concept of force balance. 

 

now what we can see that is by using the static equilibrium we can find the resultant internal
balance at any cross-section but even the name says that it is a resultant so there must be some distribution which results into this resultant so the simple static equilibrium is not alone sufficient to describe the internal distribution of force so the concept of stress is introduced to quantify these internal forces and not the resilience now what will happen when you apply the load the shape  of track it or any Mambo will change so it will deform thus the concept of strain is introduced to predict the deformation in detail so what you can say is that stress and strain are related to each other and the dependency is established using the experiment stress and strain test so in this lecture we are going to cover stress in detail and in our subsequent lecture we will we will cover these three so let's start from a journey and yeah so

 

stress are categorized as normal stress and the shear stress so normal stress from the name only you can say that they are normal to the surface and also the I think the most more appropriate name is an X zero stress and the second one is the shear stress which is parallel to this surface now first visualize this and then will express this mathematically so to understand this let us take a very simple case of bar and I am subjecting this bar with an axial loading off B so let's take this here P load is acting and same P load X P load is acting here so this here is P and here also it's P okay so in order

 

to understand the conception of battery let's draw lines on this structure before application of the load like just assume that right now I'm not applying the load P so I'll draw the lines here hmm yeah so these lines are uniformly distributed as you can see now what I'm doing is I'm applying and I will I will I will observe here like your how these lines are changing due to the application of load now load P is applied and see what you can see here is that the lines it'll near to the circular holes are not uniform but the lines that are in the middle they are uniform but what will happen when you will use the method of section you will get the same resultant at each section okay so now I'll

 

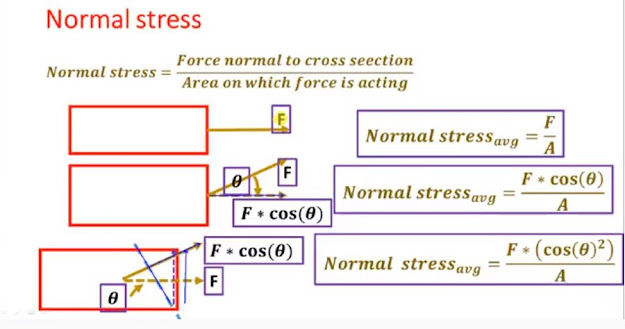
Express this or access all these things mathematically so let's go to the mathematical definition of normal stress so normal stress is the force normal to the cross section
divided by the area on which the forces acting so this area is the cross sectional area okay so if it is a rectangular bar it is the area of a
rectangle if it is a circular bar bar that will be a area of a circle okay so one point to understand is that it is area on which the forces acting so let us take a very basic example to understand this and let's assume a rectangular box of your neck thickness so for simplest case assume that the force is acting perpendicular to the area so the normal stress will be now f divided by e so here the force is here the force is f here and the area is the area of the rectangle now just so what will be the stress here normal stress average is equals to F divided by a now let's add more complexity to it by applying of force which is inclined to some surface okay so now if I'm saying
that Terr F is acting at an angle theta to the horizontal so what will be the normal or horizontal component of this
so the horizontal component of this is this thing it will be F cos theta right an area we see we need to consider area which is perpendicular to the force so the area perpendicular to this F cos theta is same it will be 8 so again our normal stress average will be F cos theta divided by E now I'm adding more complexity to the situation what else doing is I'm considering this inclined surface so this is the inclined surface that is in blue line or let me mark this yeah this is inclined surface on which I am taking D I'm calculating the known average stress so what you do here is our force is acting now our force is acting at an angle at other horizontally it is acting but we need to take the inclined section so what will be our force which is inclined to this it will be this thing it will be F cos theta so this will be the F cos theta similarly this is a right this is a so this will
be a cos theta okay so what will happen our normal stress will come it will come as F cos theta divided by a divided by cos theta so it will come as F cos theta square okay so this is a basic geometry
so you can pause the video and can try this you will also get the same result let's see here everywhere I'm mentioning is what I mentioning is normal stress average so what is the difference
between the distributed stress and the normal stress so let's move further and try to understand this thing so,

now I'm considering on random structure  now in this case let's take an elementary area Delta a

 

so this is the elementary area Delta a on which del F is acting so what you can define is that the normal stress is equals to limit Delta a tends to 0 and del F divided by Del E now what do you mean by that Delta a tends to 0 it it simply means that stresses stress are defined at a point now what you can say that this is for one point right similarly you can define this for this

point for this point and so on so if you'll take a resultant of all these normal stresses what you will get is a norm average normal stress whose resultant will be F and area is so this FX is a resultant of all the small small Delta Force and on all the forces that are acting on this random structure and we'll we will study this in in detail when we will do the same thing in principle now let's examine this and create a detail the relationship between the distributed stress and the visible so if we write the stress in the differential form the stress will be the del F divided by D Delta now just

 

So what will be the del F del F will be the Sigma multiplied by their time now if you want to calculate the total force you need to integrate this equation correct so you'll integrate the elementary force over the whole area and so what you will get is FX is equals to integration of Sigma into Delta now let's assume that FX is a resultant force which is where like and we are you're converting this distributed force
into the average one so FX is they look a resultant force which is acting at a distance of Z are from the y axis and yare from the z axis
so let me mark the locations here see this is the Zed R which is at a distance of like which is we've thought we are measuring from by X's and this is wire now FX you can calculate but it is not like it is acting at any random position it has some specific position so how you will calculate this so to find what we will do is we will do the moment balance Y moment balance because there is no  external load at the internal boundary therefore the next movement must be zero so what is the next step you need to do the movement balance and you can find the Z R and the y R that means you can find where this FX is acting so let's write the moment balance equation now my FX is acting in a distance of Zr and similarly here my F that that we are and that we have defined here is acting at a distance offset okay so what we have to do that the moment created by this
resultant force it should equate the moment created by this internal and distributed force then then then only this is our structure is an equilibrium right so if you liquid this this FX x zr that will be the moment FX is a force and there is a perpendicular distance so FX x zr equals to Sigma da into Z and then you have to integrate it how C as you can see here DF is equals to Sigma into da correct so this is the DF that is a force and force which is acting at a distance of Z so force multiplied by Z is the movement and since it is a distributed moment you are integrating it over the area a so when you solve this what you will get here is Z similarly this FX this FX is also creating a moment about the z axis right so again to find the location vy are
what you will do is the movement balance again so what what equation will come is yr x f that is a moment by the resultant force
is equals to negative offs again we are to be are doing the same thing Sigma into da that is a force multiplied by its area and then again you are integrating so again this is the force that we have done before y is again the distance that I know I'm not marked while any must see this is y so y is again the distance and you are integrating it integrating with for the area is forgetting a total moment of the distributed force and then you are equating it with this external for this soil or not external for this resultant force okay so using this what you can find is zr and via and this minus

 

reserves this is just the sign convention so if you're considering clockwise is positive then automatically anti clockwise anti-clockwise will come as negative okay so using this Portugal final radar and wire so that means you first you can find the resultant force and then you can find the location of the resultant force so both things are done now let's consider a case where I'm saying that George normal stresses distributed over the cross section so if your normal stress is distributed over the cross section your distributed force will also be or will be it will be constant okay so forth is a special case where your normal stress distribution is constant over a cross section your ethics will be the integration of SigmaX into D a and a now I'm saying that stress is constant that means you can take Sigma X outside so what will come here is this equation so FX is equals to Sigma X since it's a constant and integration of da which will give you FX is equals to Sigma X multiplied by it now using that using the previous equation that we have find out again you will take use X Sigma X or in the Sigma X outside since it's a constant value what you will get is no if you see this this dump this dump if you'll see this term so can you relate this term with the first moment of inertia and you will get here is Sigma so is that cg x the integration of PA this is our 11 standard physics so if you're not getting this just turn some pages so what what will be our final equation it will come at Z da into FX is equals to Sigma X into Z Z Z Zed of CG sorry so this FX and Sigma X and a this we have already calculated here first first thing only this these are these things are equal so that means you can cancel those things so what you will get is Z R is equals to Z CG so what is the conclusion here the conclusion here is your Z R is equals to z cg only and only if your normal stress is uniform over the cross-section that means if your normal stress is uniform over the cross section it will act at least centroid of cross section one more thing we need to consider here is the length of the bar see if if your cross section is varying along the length of the bar then this this conclusion that we have made is not well it so we will see that in upcoming lectures but for now you can say that okay if your bar is uniform your force for your resultant force will act at the CG of the bar

 

 

 okay the CG of the cross section so what are the conditions for the uniform normal stress and by yeah so first thing is okay so the first thing is that your bar should be prismatic prismatic means that this area should be constant along the length then it should be homogeneous that it should be it should be the same material then equal and opposite load P or anything that is acting it should it should be equal on the both sides then your resultant force will act at the center then resultant force at centroid of cross-section automatically if all these training three things are there then your resultant force will act at the center of cross-section we have already proved this in our in the plus section only so we have covered everything about the basics of normal stress so let's solve a problem and what if you have any doubt I think they will be gone after after that okay

 

so what is the 

Example 

 

now two rods are there which are welded at a point B to form a single rod the 30 kilonewton force at B is uniformly distributed around the circumference of collar at B and a 10 kilo Newton load is applied at C and also it is a cross section of the classify centroid of the cross section so now what we have to find is the XEL stress in each portion of rotten so now let's pause for a moment and check that the assumption for nor uniform stress whether they are valid here or not now you can see that all the points are valid but for that we need what we need to do is we need to divide this bar into two portions like a b and b c and then only over all points are valid and this is what we are going to do because we are ignoring the same Venant effect here for now we are ignoring that effect and we are going to separate this bar into two to two sections and we are going to solve this so to understand this let's start solving the problem by considering the free body diagram of bus individually now set design conventions we are taking pension is positive so let's solve the problem find these strips so first make the free body diagram here this is the other view so your first section the c section 10 kilonewton if you'll divide this you will get f1 on the other side then 

 

now at Point C then new genus acting that is as a friend so from point B to C what will what what what what force will act is the 10 kilonewton so you can see you can check here is still still bu the only for unknown force what we have is ever but at Point a junction of B when you'll divide this what you'll get is f 2 that means we have two forces F 1 and F 2 when you are dividing the body into two portions so what we need to do is we need to find this F 1 and F 2 so let's start so using force barons along the cut line that means in the first section if 10 kilonewton is acting in this direction that is tension so that means F 1 also it saw it is also a positive force only so what you'll get F 1 as the 10 kilonewton

 

because what equilibrium f 1 should equal to 10 kilonewtons so whatever is a demon whatever whatever whatever is the diameter of Part B see you will calculate the area so what will come it is the area of the cross section so it will come as PI by 4 D 1 square so your stress will come with ya so your Exia stress in BC will be equal to F 1 divided by a 1 where Ava is equals to PI by 4 into D 1 square right now you need to go for this VC not since force is acting at point B you nee you don't know like what how much is the resultant force is acting at point B so you need to calculate that first what you can do here is see your 10 kilonewton force is acting in this direction which we have taken as positive and then the 30 kilo
Newton is acting in this direction okay so this is the 10 kilo Newton let me mark this this is the 10 kilo Newton and this is the Kappa kilo Newton right so what is the resultant force so
we'll take from the positive direction only so what you'll get here is the f2 is equals to 10 kilonewton - of 30 kilonewton so it will come as a minus of 20 kilo Newtons similarly what does the area it with it is C D 1 is not equals to D 2 okay so your area will come as a 2 will come as PI by 4 D 2 square so if D 1 and D 2 are known to you so you know if it is like this there if it is like this body just
separate the body if either either in 1/2 or if it is 3 section also you can separate the body in 3 halves at every Junction do the force balance and calculate the axial stresses okay so this was the first problem we have done in the subsequent lectures we will cover some more problem so that you are all doubts will be cleared okay thank you and if you liked the video please subscribe for more interesting videos

thank you